数组实现线段树

常规线段树，数组实现！！！

问题

例题 数组区间内最小值、最大值、总和等问题；

定义

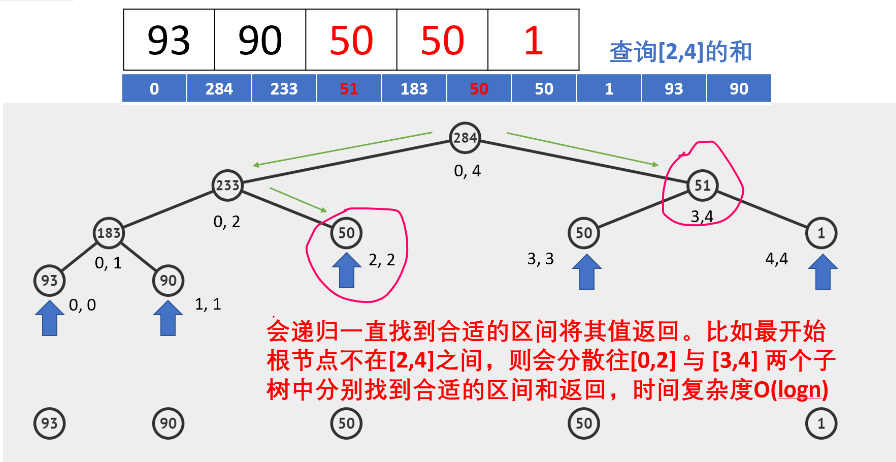
• 线段树 segmentTree 是一个二叉树，线段树可以用树也可以用数组（堆式存储）来实现。
• 线段树结构有点像堆，一般用数组来表示线段树的结构；
• 在index = 0的位置保存根节点，则左子节点是2 * index + 1,右子节点是2 * index + 2;
• (若在index = 1的位置保存根节点，则左子节点是2 * index,右子节点是2 * index + 1)
• 线段树中每个节点都表示一个区间的信息，如数组 nums 在区间 [s, e] 的最小值、最大值或总和等信息。
• 以区间总和为例，根节点存储所有元素的和；
• 原数组中的每一个元素都以叶子节点的形式存在于线段树中；
• 主要有3个操作：建树、查询、更新；
• 线段树将此类问题的查询以及更新的时间复杂度都变成了O(logn)；

实现

以区间总和为例！！！

• start、end、left、right表示nums中的下标；
• [left, right]是检索区间；
• [start, end]是当前区间；
• node_idx表示线段树中的节点的下标；

建树

class NumArray {
private:
    // 原数组大小为n;
    int n;
    // 用数组表示线段树，规定根结点 0 保存区间 [0,n−1] 的总和
    vector<int> segmentTree;
public:
    //线段树大小不过4n，建树
    NumArray(vector<int>& nums) : n(nums.size()), segmentTree(4 * nums.size()) {
        build(nums, 0, n - 1, 0);
    }
    //更新
    void update(int index, int val) {
        change(index, val, 0, n - 1, 0);
    }
    //查询
    int sumRange(int left, int right) {
        return query(left, right, 0, n - 1, 0);
    }
};
void build(vector<int>& nums, int start, int end, int node_idx){
    if(start == end){
        segmentTree[node_idx] = nums[start];
        return;
    }
    int mid = start + (end - start) / 2;
    int left_node_idx = node_idx * 2 + 1;
    int right_node_idx = node_idx * 2 + 2;
    build(nums, start, mid, left_node_idx);
    build(nums, mid + 1, end, right_node_idx);
    segmentTree[node_idx] = segmentTree[left_node_idx] + segmentTree[right_node_idx];
}

查询

根据区间范围从根节点递归地向树的两边查询；

int query(int left, int right, int start, int end, int node_idx){
    if(right < start || left > end){//当 检索区间 在 当前区间 左边或右边时
        return 0;
    }else if(left <= start && end <= right){//当 检索区间 包括 当前区间 时
        return segmentTree[node_idx];
    }else{
        int mid = start + (end - start) / 2;
        int left_node_idx = node_idx * 2 + 1;
        int right_node_idx = node_idx * 2 + 2;
        //mid在变，而检索区间不变，所以传参数时left、right不变，start、end在变
        return query(left, right, start, mid, left_node_idx) + 
               query(left, right, mid + 1, end, right_node_idx);
    }
}

更新

从对应的叶子节点开始更新到根节点；

//index是给定数组的将改变元素的下标，val是对应值
void change(int index, int val, int start, int end, int node_idx){
    if(start == end){
        segmentTree[node_idx] = val;
        return;
    }
    int mid = start + (end - start) / 2;
    int left_node_idx = node_idx * 2 + 1;
    int right_node_idx = node_idx * 2 + 2;
    if(index <= mid){
        change(index, val, start, mid, left_node_idx);
    }else{
        change(index, val, mid + 1, end, right_node_idx);
    }
    segmentTree[node_idx] = segmentTree[left_node_idx] + segmentTree[right_node_idx];
}